308 Range Sum Query 2D - Mutable

308. Range Sum Query 2D - Mutable

1. Question

Given a 2D matrixmatrix, find the sum of the elements inside the rectangle defined by its upper left corner (row1,col1) and lower right corner (row2,col2).

The above rectangle (with the red border) is defined by (row1, col1) =(2, 1)and (row2, col2) =(4, 3), which contains sum =8.

Example:

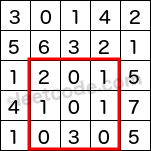
Given matrix = [
  [3, 0, 1, 4, 2],
  [5, 6, 3, 2, 1],
  [1, 2, 0, 1, 5],
  [4, 1, 0, 1, 7],
  [1, 0, 3, 0, 5]
]

sumRegion(2, 1, 4, 3) -> 8
update(3, 2, 2)
sumRegion(2, 1, 4, 3) -> 10

Note:

1. The matrix is only modifiable by the update function.

2. You may assume the number of calls to update and sumRegion function is distributed evenly.

3. You may assume that row 1 ≤ row2 and col1 ≤ col2.

2. Implementation

(2)2D Binary Indexed Tree

思路: 二维的树状数组其实相当于每一行都是一个binary indexed tree

class NumMatrix {
    BIT bit;
    int m;
    int n;
    int[][] nums;

    public NumMatrix(int[][] matrix) {
        if (matrix == null || matrix.length == 0) {
            return;
        }
        this.nums = matrix;
        m = matrix.length;
        n = matrix[0].length;
        bit = new BIT(m, n);

        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                bit.update(i, j, matrix[i][j]);
            }
        }
    }

    public void update(int row, int col, int val) {
        int diff = val - nums[row][col];
        nums[row][col] = val;
        bit.update(row, col, diff);
    }

    public int sumRegion(int row1, int col1, int row2, int col2) {
        return bit.query(row2 + 1, col2 + 1) - bit.query(row2 + 1, col1) - bit.query(row1, col2 + 1) + bit.query(row1, col1);
    }
}

class BIT {
    int[][] sums;

    public BIT(int m, int n) {
        sums = new int[m + 1][n + 1];
    }

    public void update(int row, int col, int val) {
        for (int i = row + 1; i < sums.length; i += (i & -i)) {
            for (int j = col + 1; j < sums[0].length; j += (j & -j)) {
                sums[i][j] += val;
            }
        }
    }

    public int query(int row, int col) {
        int sum = 0;
        for (int i = row; i > 0; i -= (i & -i)) {
            for (int j = col; j > 0; j -= (j & -j)) {
                sum += sums[i][j];
            }
        }
        return sum;
    }
}

/**
 * Your NumMatrix object will be instantiated and called as such:
 * NumMatrix obj = new NumMatrix(matrix);
 * obj.update(row,col,val);
 * int param_2 = obj.sumRegion(row1,col1,row2,col2);
 */

3. Time & Space Complexity

Binary Indexed Tree: 时间复杂度: Binary Indexed Tree创造: O(m * logm * n * logn), update: logm * logn, query: logm * logn